[박정현의 데이터사이언스 시작하기] ⑪ 성능평가 (2) - 분류 < 박정현의 데이터사이언스 < 오피니언 < 기사본문

이제 분류 모델이 어떤 일을 하는지 생각해보자. 분류 모델은 훈련 데이터를 학습해서 테스트 데이터가 입력됐을 때 학습한 내용을 바탕으로 어떤 범주(Class)로 분류되는지 예측한다. 이때 예측한 범주와 실제 범주가 같다면 우리가 만든 모델이 제대로 작동했다고 생각할 수 있을 것이다.

분류 모델에서는 이처럼 모델이 여러 번 예측을 수행해서 예측한 결과가 맞은 경우와 틀린 경우를 바탕으로 모델의 성능을 평가하게 된다.

이진 분류의 경우 Positive와 Negative 2개의 값을 예측하는 경우이므로 실제 Positive인 값을 Positive로 예측할 수도 있고, Negative로 예측할 수도 있다.

또 Negative를 Negative로 예측할 수도 있으며 Negative를 Positive로 예측할 수도 있다.

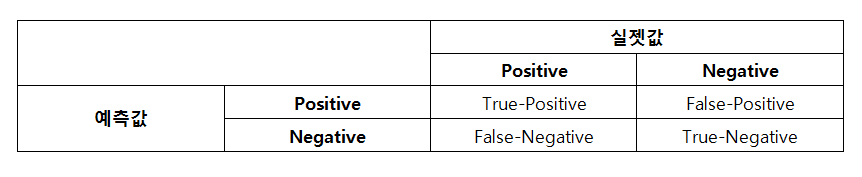
Positive를 Positive로 분류한 경우(True-Positive)와 Negative를 Negative로 분류한 경우(True-Negative)는 모델이 제대로 작동한 경우일 것이며, Positive를 Negative로 분류(False-Negative)하거나 Negative를 Positive로 분류(False-Positive)한 경우 에러라고 생각할 수 있다.

(True/False)-(Positive/Negative) 형식에서 뒷부분의 Positive/Negative가 분류를 어떻게 예측했는가를 나타내며, 앞부분의True/False가 이때 예측한 분류가 맞았는지 틀렸는지를 나타낸다고 보면 된다.

이를 정리하면 아래 표와 같으며 이를 혼동행렬(Confusion Matrix)라고 한다.

성능지표들

회귀 모델에서 오차를 사용해 여러 지표를 만들었던 것과 비슷하게 분류 문제는 혼동 행렬을 바탕으로 다양한 성능 지표를 계산한다. 가장 기본이 되는 모델의 정확도는 다음과 같이 표현할 수 있다.

정확도(accuracy) = 예측한 것들 중 맞춘 분류의 수/전체 예측한 횟수 = (TP+TN)/(TP+FP+FN+TN)

예를 들어 코로나19 감염 여부를 분류하는 검사를 만들어 100명을 검사한 결과가 다음과 같다고 하자.

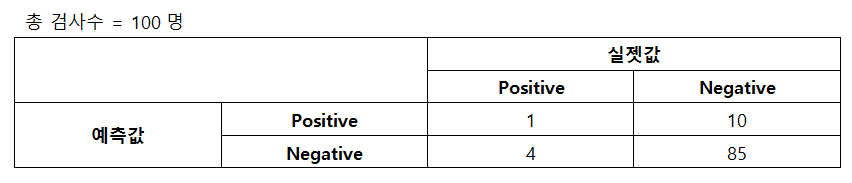
이때 정확도는 (4+85)/100=90%가 된다. 100점 만점에 90점의 점수는 우수한 점수라고 생각할 수 있다. 하지만 실제 코로나19에 감염된 사람을 얼마나 잘 찾아냈는지(True-Positive) 확인해보자. 100명 중 실제 감염자는 5명이었으며 이때 검사를 통해 1명은 감염자를 발견했지만 4명의 감염자를 비감염자로 분류하는 오류가 나타났다.

이러한 문제는 범주별로 데이터의 분포가 고르지 않기에 나타나게 된다. 다시 말해 코로나19 검사의 경우 대부분의 사람들이 비감염자(Negative)이고 일부만 감염자이기에 만약 검사 시 모두 비감염이라고 해도 정확도(accuracy)는 90% 이상을 보이게 되는 것이다.

따라서 이러한 문제를 보완하기 위해 recall과 precision이라는 성능지표를 사용하게 되며 각각은 다음과 같이 계산한다.

Recall = 실제 Positive 중 Positive로 분류된 비율 = TP / (TP+FN) = 1 / (1+4) = 0.2(20%)

Precision = Positive로 분류한 경우 중 실제 Positive의 비율 = TP / (TP/FP) = 1 / (1+10) = 0.09(9%)

이처럼 정확도가 90%임에도 실제 Recall과 Precision은 낮은 성능을 보이는 것을 알 수 있다. 이를 보완하기 위해 특히 불균형한 데이터(Imbalanced Dataset)의 경우 Recall과 Precision의 조화 평균인 F1-score를 사용하며 식은 다음과 같다.

F1-Score = 2* (Recall * Precision) / (Recall + Precision)

분류의 경우 대상에 따라 어떠한 성능 지표를 사용하는지가 더욱 중요할 수도 있다. 예를 들어 신용카드 사기 거래를 검출하는 모델을 생각해보자.

만약 모델이 사기 거래를 사기가 아닌 것으로 분류(False-Negative)인 경우 회사가 손해를 입게 된다. 반면 사기 거래가 아닌 경우를 사기로 분류(False-Positive)하게 되면 고객 카드 중지와 같은 일이 발생해 고객에게 손해가 된다.

따라서 이러한 경우 회사의 입장에서는 FN가 중요한 수치이기에 Recall이 중요한 지표일 수 있으며, 고객의 입장에서는 FP가 중요한 수치로 Precision에 더욱 민감할 것이다.

ROC(Receiver Operating Characteristic)와 AUC(Area Under Curve)

그러나 실제 분류 모델의 경우 단 하나의 기준으로 분류할 수는 없을 것이다. 예를 들어 검사를 위해 채취한 침에 코로나 바이러스가 1개만 있어도 Positive로 분류할 것인지 100개 이상인 경우 Positive로 감염자로 분류할 것인지 등 임계치(threshold) 값을 가질 수 있다.

각각의 임계치 마다 검사 결과를 혼동행렬로 표현할 수 있으며 이를 활용해 ROC를 나타낼 수 있는데 ROC의 가로축과 세로축은 다음과 같이 정의한다.

가로축 = FPR(False Positive Rate) = 1 – TNR(True Negative Rate) = 1 - Specificity

세로축 = TPR(True Positive Rate) = Recall = Sensitivity

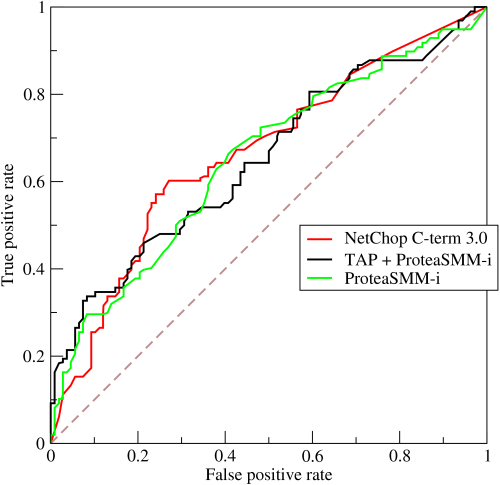
임계값을 변경하면서 혼동행렬을 구해 TPR과 FPR을 계산해 그림으로 표현하면 위와 같은 곡선을 갖게 되며 이를 ROC 곡선이라 한다.

위 ROC 곡선들을 보면 대각선 점선을 기준으로 왼쪽 위를 향하게 된다. 왼쪽 최상단이 의미하는 바는 TPR이 1이고 FPR이 0인 값으로 가장 좋은 성능을 보인 경우라 할 수 있다. 따라서 ROC 곡선이 왼쪽 위를 향할수록 우수한 성능을 보이는 모델이다.

이를 좀 더 정확하게 계산하기 위해 곡선의 아래 부분의 면적을 계산한 지표가 AUC(Area Under Curve)이며 이 역시 가로 세로가 각각 1인 경우 면적이 1로 가장 우수한 성능을 의미한다.

예제에서 살펴본 것과 같이 같은 모델의 결과라 하더라도 고객의 관점에서 혹은 기업의 입장에서 더 민감한 지표가 있음을 알 수 있었다.

따라서 실제 우리가 모델을 만들 때에도 이러한 점을 고려해 어떤 지표를 높이는 것을 목표로 할지 생각해봐야 할 것이다.

또한 데이터의 분포가 범주별로 다른 경우 단순히 정확도를 사용하는 것을 조심해야 하며, 불균형한 데이터세트의 경우 샘플링(Sampling) 혹은 오버샘플링(Over-Sampling)을 통해 데이터세트를 새로 구성해 활용하는 등의 작업이 필요할 것이다.

다음 시간에는 마지막으로 실제 데이터분석과 관련된 현업 전문가와 간단한 인터뷰를 통해 우리가 배운 지식을 실무에 적용해 볼 수 있는지 어떤 부분을 더 준비해야 하는지 알아보는 시간을 갖고자 한다.

박정현 칼럼니스트는 서울대 EPM연구원(공학전문대학원 엔지니어링 프로젝트 매니지먼트(EPM) 연구실)이며, 머신러닝 스타트업을 창업한 바 있다.

박정현 서울대학교 연구원 park.jeonghyun@snu.ac.kr