[박정현의 데이터사이언스 시작하기] ⑧ 알고리즘 (2) - 분류

분류분석

데이터 분석의 문제는 크게 회귀 분석과 분류 분석 문제 두 가지 종류라고 볼 수 있다. 물론 다음 주에 설명할 군집화(clustering)를 또 다른 하나의 데이터 분석 분야로 설명할 수 있다. 이번 시간에는 지난번 글에서 설명한 회귀 분석에 이어 분류 분석에 대해 설명한다.

회귀분석에서 찾고자 하는 목적값이 온도, 경기 지표, 부동산 가격과 같은 숫자로 표현할 수 있는 값이라면, 분류분석에서 찾고자 하는 목적값은 질병 감염 여부를 음성/양성으로 구분하거나 이메일의 스팸 여부를 구분하는 이진분류, 고객의 등급을 여러 등급으로 분류하는 경우와 같은 것이다. 이처럼 이미 알고 있는 데이터의 레이블링 값을 통해 새로운 데이터가 어떠한 범주로 분류되는지 예측하는 문제들을 분류 분석이라 할 수 있다.

로지스틱 회귀

분류문제를 해결하는 방식 중 가장 많이 사용되는 로지스틱 회귀(logistic regression)에 대해 알아보자. 지난 시간에 살펴본 선형 회귀의 경우 찾고자 하는 값이 연속적인 수치형 값으로 표현되었다. 로지스틱 회귀도 계산하는 방식이 유사하지만 연산 마지막 단계에 시그모이드(sigmoid) 함수를 사용해 결괏값을 0과 1 사이의 값으로 변환

해 사전에 설정한 임곗값을 기준으로 0과 1의 이진값으로 분류하게 된다.

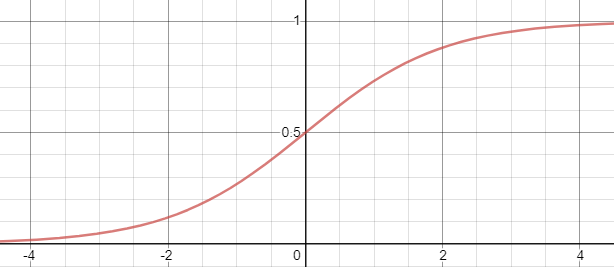
아래 그림은 시그모이드 함수의 그래프로 -무한대에서 +무한대의 입력값을 0과 1사이의 값으로 변환해주는 것을 확인할 수 있다. 인공 신경망에서는 비슷한 원리로 tanh 함수, ReLU(Rectified Unit) 등을 사용해 신호를 다음 단계로 전달할지 여부를 결정하는 활성화함수로 사용한다.

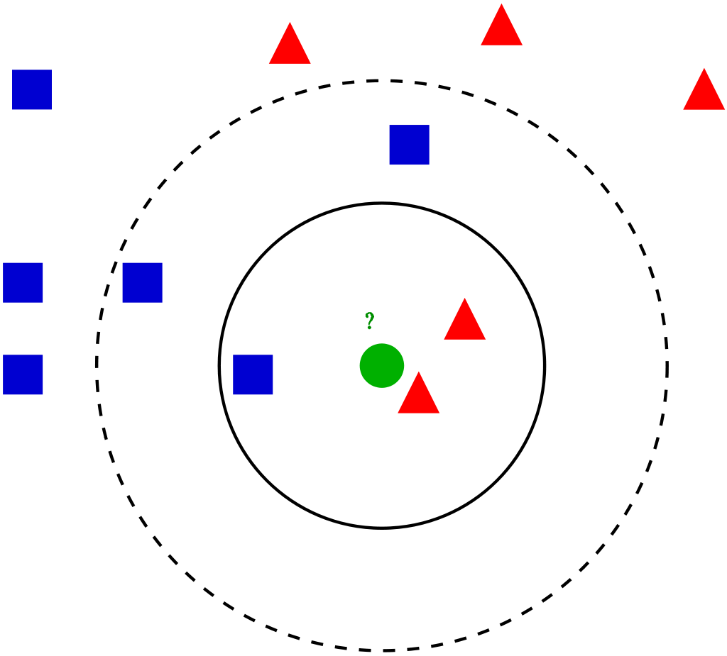
K-NN(K nearest neighbor) 알고리즘

분류 문제를 해결하는 대표적인 방식이 K-NN 방법이다. K값은 사용자가 지정해주는 값으로 분류하고자 하는 데이터와 가장 가까운 K개의 데이터를 찾아서 어떤 범주에 많이 속하는지를 분석해 입력된 데이터를 분류하는 방식이다.

위키피디아에서 가져온 사진을 예를 들어 설명해보자. 데이터 세트에는 파란 네모와 빨간 세모 2가지의 범주가 존재한다. 이때 새로운 입력값 녹색 동그라미를 어느 쪽으로 분류해야 할까? K값을 3, 5로 정했다고 가정하고 설명해보자.

◆K=3일 때

K값이 3이므로 입력값인 녹색 동그라미와 가장 거리가 가까운 3개 데이터를 찾아보면 검정 실선으로 표시된 원 안에 있는 점 3개로 2개의 빨간 세모와 1개의 파란 네모 1개임을 알 수 있다. 따라서, K=3일 때 입력값 녹색 동그라미는 빨간 세모 범주로 분류된다.

◆K=5일 때

K값이 5인 경우에도 위와 같은 방식으로 입력값 녹색 동그라미와 가장 가까운 5개의 데이터를 찾는다. 이는 검은색 점선으로 표시된 원 안에 존재하는 데이터들로 파란색 네모 3개와 빨간색 세모 2개임을 알 수 있다. 따라서, 이번에는 K=3일 때와 다르게 녹색 동그라미를 파란 네모 범주로 분류하게 된다.

이처럼 K-NN의 K값은 사용자가 지정하는 값으로 어떻게 정하는지에 따라 다른 결과를 보일 수 있다. 그리고 범주별로 동일한 개수의 데이터가 있을 수 있어 보통은 K값을 1, 3, 5와 같이 홀수로 정하는 것이 일반적이다.

이 밖에도 의사결정 나무(decision tree), SVM(support vector machine) 등과 같이 다양한 알고리즘을 사용해 분류 문제를 해결한다. 참고로 선형회귀를 활용해 로지스틱 회귀로 분류 문제를 해결하는 것과 같이 의사결정 나무 방식을 변형해서 회귀 문제를 해결할 수도 있다.

박정현 서울대학교 연구원 park.jeonghyun@snu.ac.kr

[관련 기사][박정현의 데이터사이언스 시작하기] ⑦ 알고리즘 (1) - 회귀

[관련 기사][박정현의 데이터사이언스 시작하기] ⑥ 피처 엔지니어링 (2)