대형언어모델(LLM)이 귀납적 추론에는 강하지만, 연역적 추론에는 매우 약하다는 연구 결과가 나왔다. 이런 점은 LLM의 한계와 사용법에 대한 중요한 참고가 된다는 설명이다.
벤처비트는 15일(현지시간) 아마존과 캘리포니아대학교 로스앤젤레스(UCLA) 연구진이 LLM에 대한 연역 및 귀납적 추론 능력에 대해 포괼적인 연구를 수행했다고 보도했다.
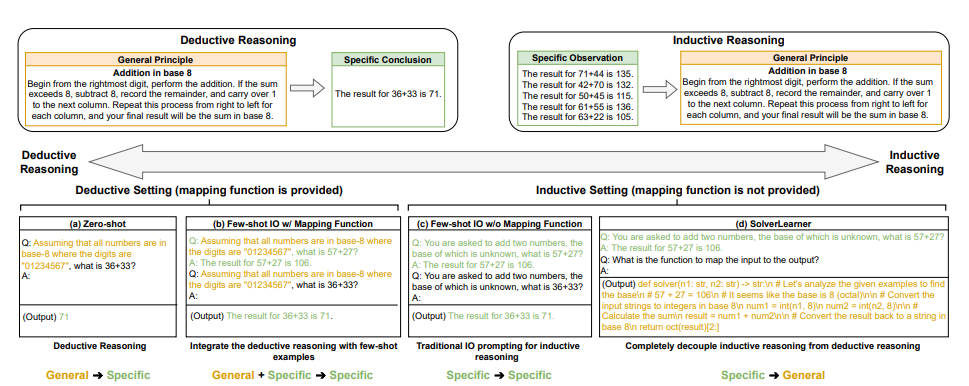
추론은 일반적으로 귀납과 연역 두가지로 나눈다. 귀납은 개별적인 특수한 사실이나 현상에서 보편적이며 일반적인 결론을 끌어내는 방식이다. 반대로 연역은 일반적인 원칙이나 가정으로 시작, 이를 특정 결론을 내는 것으로 확장한다.
두가지 추론 모두 지능에는 필수적인 요소다. 하지만 LLM의 추론 능력을 측정하는 과정에서는 둘을 구분하는 경우가 거의 없었다는 지적이다.
따라서 연구진은 LLM의 귀납적 및 연역적 추론 능력을 평가하기 위한 실험을 설계했다. 유사한 과제 구조를 갖췄지만, 서로 다른 맥락에서 연역 또는 귀납적 추론을 특별히 강조한 장치다.
구체적으로 LLM이 주어진 수학적 함수를 적용해 문제를 해결하는 능력(연역적 추론)과 일련의 입출력 예제에서 기본적인 수학적 함수를 추론하는 능력(귀납적 추론)을 테스트했다.
또 이를 더 정확하게 판정하기 위해 LLM에서 귀납적 추론 과정을 분리해 평가하는 2단계 프레임워크인 '솔버러너(SolverLearner)'를 개발했다. 즉, 귀납 과정만을 따로 평가, 전체 추론 결과에서 귀납과 연역 능력이 차지하는 비중을 평가한 것이다.

이를 사용해 'GPT-3.5'와 'GPT-4'를 평가한 결과, 두 모델은 귀납적 추론에서는 놀라운 능력을 발휘했다고 전했다. 이와 같은 '패턴 분석'은 LLM의 특징이다.
반면 연역에서는 상당한 어려움을 겪은 것으로 나타났다. 특히 주어진 지침이 훈련 중 일반적으로 주어지지 않는 경우는 더 심했다는 분석이다. 예를 들어 익숙한 10진법 연역에서는 비교적 좋은 성적을 거뒀으나, 9진법이나 11진법처럼 흔하지 않은 경우에는 매우 성적이 낮았다고 밝혔다.
따라서 LLM은 명시적 지침을 따르는 것보다 예제를 통해 학습하고 데이터에서 패턴을 발견하는 데 더 능숙하다는 결론이다.
또 이는 실제 시나리오에서 LLM을 사용하는 데 중요한 의미를 갖는다고 덧붙였다. 겉보기에는 LLM이 논리적 지침을 따르는 것처럼 보일 수 있지만, 이는 사실 훈련 중 관찰한 패턴을 따르고 있을 가능성이 높다는 점이다. 또 LLM이 처리하는 예제가 훈련 분포에서 벗어나면 성능이 떨어진다는 것을 의미한다.
한편, 이번 실험에 사용한 솔버러너와 같은 도구는 LLM 출력을 분석하는 좋은 프레임워크가 될 수도 있다. 하지만 코드 인터프리터와 같이 검증 메커니즘을 사용할 수 있는 구조에서만 적용할 수 있다는 한계가 있다.
LLM이 패턴 학습에 특화했다는 것을 감안하면 이번 연구 결과는 당연한 것으로 볼 수 있다. 이에 대해 벤처비트는 "이런 LLM의 블랙박스의 능력에 대해 우리가 아직 배워야 할 것이 많다는 점을 냉정하게 일깨워 준다"라고 평했다.
임대준 기자 ydj@aitimes.com